Difference between revisions of "Upwelling diffusion climate model"
(Created page with "*model description ** carbon cycle ** non-CO2 concentrations **[[Radiative Forcing | radiative forcing r...") |
(No difference)
|
Revision as of 13:29, 17 June 2013
From forcing to temperatures: the upwelling-diffusion climate model
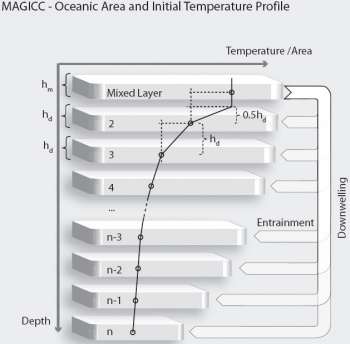
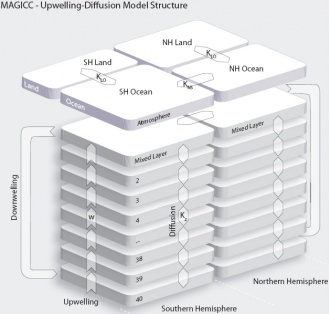
In the early stages, MAGICC's climate module evolved from the simple climate model introduced by Hoffert et al. (1980). MAGICC's atmosphere has four boxes with zero heat capacity, one over land and one over ocean for each hemisphere. The atmospheric boxes over the ocean are coupled to the mixed layer of the ocean hemispheres, with a set of n-1 vertical layers below (see Fig-A3). The heat exchange between the oceanic layers is driven by vertical diffusion and advection. In the previous model versions, the ocean area profile is uniform with depth and the corresponding downwelling is modeled as a stream of polar sinking water from the top mixed layer to the bottom layer. In this study, an updated upwelling-diffusion-entrainment (UDE) ocean model is implemented with a depth-dependent ocean area (from HadCM2). For simplicity, the following equations govern the uniform area upwelling-diffusion version of the model. The upwelling-diffusion-entrainment implementation section provides details on the UDE algorithms.
Partitioning of feedbacks
In order to improve the comparability between MAGICC and AOGCMs, and following earlier versions of MAGICC, we use different feedback parameters over land and ocean. This requires an adjustable land to ocean warming ratio in equilibrium based on AOGCM results. Given that in equilibrium the oceanic heat uptake is zero, the global energy balance equation can be written as:
<m>C\Delta Q_G=\lambda_G\Delta T_G=f_{L}\lambda_L \Delta T_{L} + f_{O}\lambda_O \Delta T_{O}\label{eq_globalenergybalance_equilibrium}</m>where <m>\Delta Q_G</m>, <m>\lambda_G</m> and <m>\Delta T_G</m> are the global-mean forcing, feedback, and temperature change, respectively. The right hand side uses the area fractions <m>f</m>, feedbacks <m>\lambda</m>, and mean temperature changes, <m>\Delta T</m> for ocean (<m>O</m>) and land (<m>L</m>). As in earlier versions of MAGICC, the non-linear set of equations that determines <m>\lambda_O</m> and <m>\lambda_L</m> for a given set of equilibrium land-ocean warming ratio <m>RLO</m>=<m>\Delta T_L/ \Delta T_O</m>), global-mean feedback <m>\lambda_G</m>, heat exchange and enhancement factors (<m>k</m>, <m>\mu</m>), is solved by an iterative procedure involving the set of linear Eqs. (A46-A49), seeking the solution for <m>\lambda_L</m> closest to <m>\lambda_G</m>. The procedure in version 6 has been modified slightly to take into account the time-constant radiative forcing pattern by CO2 for the four boxes with hemispheric land/ocean regions, if prescribed.
Following Wigley and Schlesinger (1985), it is assumed that the atmosphere is in equilibrium with the underlying ocean mixed layer, so that the energy balance equation for the Northern Hemispheric ocean (NO) is:
| <m>&f_{\rm NO}\lambda_{O}\Delta T_{\rm NO} =</m> | <m>\textrm{:infrared outgoing flux}</m> |
| <m>f_{\rm NO}\Delta Q_{\rm NO}</m> | <m>\textrm{:forcing}</m> |
| <m>+ k_{\rm LO}(\Delta T_{\rm NL} - \mu \Delta T_{\rm NO})</m> | <m>\textrm{:land-ocean heat exchange}</m> |
| <m>+ k_{\rm NS}\alpha(\Delta T_{\rm SO} - \Delta T_{\rm NO})</m> | <m>\textrm{:hemispheric heat exch.}</m> |
where <m>\Delta T_{\rm NO}</m> is the surface temperature change over the Northern Hemisphere ocean, <m>\Delta Q_{\rm NO}</m> the radiative forcing over that region, <m>f_{\rm NO}</m> the northern ocean's area fraction of the earth surface, <m>k_{\rm LO}</m> the land-ocean heat exchange coefficient [Wm-2<m>^\circ</m>C-1], a heat transport enhancement factor <m>\mu</m> allowing for asymmetric heat exchange between land and ocean (1<m>\leq</m><m>\mu</m> (see Sect. Revised land-ocean heat exchange formation below), <m>k_{\rm NS}</m> is the hemispheric heat exchange coefficient in the mixed layer. Following Raper and Cubasch (1996)) <m>\alpha</m> is a sea-ice related adjustment factor to relate upper ocean temperature change to surface air temperature change (see Revised land-ocean heat exchange formation). Correspondingly, the equilibrium energy balance equations for the Northern Hemisphere land (NL), Southern Hemisphere ocean (SO) and Southern Hemisphere land (SL) are:
As detailed below (Accounting for climate-state dependent feedbacks), if the sensitivity factor <m>\xi</m> is set different from zero (see Eq.A51), it is possible to make the feedback factors <m>\lambda</m> in the energy balance equation dependent on the total radiative forcing. This forcing dependence of the feedback factors and the heat exchange enhancement factors are newly introduced in this version of MAGICC. The following two sections (Revised land-ocean heat exchange formation and Accounting for climate-state dependent feedbacks) are intended to provide both the motivation and details of these new parameterizations.
Revised land-ocean heat exchange formulation
This section highlights a "geometric" effect that can cause effective climate sensitivities to change over time. The global-mean sensitivity may increase simply due to decreasing land-ocean warming ratios, given that climate feedbacks over land and ocean areas are different. To control the relative temperature changes over ocean and land, a heat transport enhancement factor <m>\mu</m> is introduced. Enhancing the ocean-to-land heat transport (<m>\mu{\geq}</m>1) has the benefit that the simple climate model can better simulate some characteristic AOGCM responses. In the idealized forcing runs, AOGCMs often show a transient land-ocean warming ratio that slightly decreases over time, but stays above unity, combined with an increasing effective climate sensitivity in some models (see bottom rows in Fig. B1, B2, and B3 in http://www.atmos-chem-phys.net/11/1417/2011/acp-11-1417-2011.html). The higher land than ocean warming (RLO<m>{>}</m>1) could be achieved by a smaller feedback (greater climate sensitivity) over land compared to the ocean boxes. However, as the land-ocean warming ratio decreases over time (due to less and less ocean heat uptake towards equilibrium), so would the effective global-mean climate sensitivity in previous model versions. The method used here, to allow both a RLO above unity and a non-decreasing effective climate sensitivity, assumes that ocean temperature perturbations influence the heat exchange more than land temperature changes. This asymmetric heat exchange formulation is then given by:
<m>{\rm HX}_{\rm LO}=k_{\rm LO}(\Delta T_{L} - \mu \Delta T_{O})\label{eq<m>eatxchange}</m>where <m>HX_{\rm LO}</m> is the land-ocean heat exchange (positive in direction land to ocean), <m>\mu</m> is the ocean-to-land enhancement factor and <m>\Delta T_L</m> and <m>\Delta T_O</m> are the temperature perturbations for the land and ocean region, respectively (cf. Eq. A46 ff.). Typical values for <m>\mu</m> range between 1 and 1.4 as estimated from calibrating the CMIP3 ensemble.
Accounting for climate-state dependent feedbacks
Some AOGCM runs indicate higher effective climate sensitivities for higher forcings and/or temperatures. For example, the ECHAM5/MPI-OM model shows an effective climate sensitivity of approximately 3.5<m>\circ</m>C after stabilization at twice pre-industrial CO2 concentrations and 4<m>\circ</m>C for stabilization at quadrupled pre-industrial CO2 concentrations (see Raper et al., 2001, Hansen et al., 2005). Given that the transient land-ocean warming ratio is the same for the 1pctto2x and 1pctto4x runs ( see Fig. B1.last row in http://www.atmos-chem-phys.net/11/1417/2011/acp-11-1417-2011.html), the 'geometric' effect discussed in the Sect. Revised land-ocean heat exchange formation would not explain this increase in climate sensitivity. An alternative explanation could be that climate feedbacks are climate-state dependent. The assumption in the standard energy balance with a constant global feedback (<m>\lambda</m>), with its attendant requirement that the outgoing energy flux scales proportionally with temperature change, may be an oversimplification. For example, the slow feedback due to retreating ice-sheets can lead to changes in the diagnosed effective sensitivities in AOGCMs (see e.g. Raper et al., 2001) over long time-scales. Hansen et al., 2005 show that the 100-year climate response in the GISS model is more sensitive to higher forcings than to lower or negative forcings. Hansen et al.~(2005) express this effect by increasing efficacies for increasing radiative forcing. Table 1 in Hansen et al., 2005 suggests a gradient of roughly 1 % increase in efficacy for each additional Wm-2 (OLS-regression of Ea versus Fa across the full range of CO2 experiments), although some intervals (e.g. from 1.25 to 1.5<m>\times</m>CO2) show a slightly higher sensitivity of efficacy to forcing, i.e., 3% per Wm-2.
Rather than making the efficacies dependent on forcing, an alternative is to make the climate sensitivity dependent on the forcing level. This distinction, on whether to modify forcing or sensitivity, is not important when the climate system is at or close to equilibrium. However, if the efficacies of the forcing, instead of the feedback parameters are allowed to vary with forcing, the transient climate response after a change in forcing will be slightly faster. In this MAGICC version, if a forcing dependency of the sensitivity is assumed, the land and ocean feedback parameters <m>\lambda_L</m> and <m>\lambda_O</m> are scaled as
<m>\lambda =\frac{\Delta Q_{2x}}{\frac{\Delta Q_{2x}}{\lambda_{2x}}+\xi(\Delta Q- \Delta Q_{2x})} \label{eq_feedback_dependency_forcing}</m>where <m>\lambda_{2x}</m> is the feedback parameter (=<m>\frac{\Delta Q_{2x}}{\Delta T_{2x}}</m>) at the forcing level for twice pre-industrial CO_2 concentrations. The sensitivity factor <m>\xi</m> (KW-1m2) scales the climate sensitivity in proportion to the difference of forcing away from the model-specific "twice pre-industrial CO<m>_2</m> forcing level" (<m>\Delta Q{-} \Delta Q_{2x}</m>). The 1% increase in efficacy for each additional unit forcing in Hansen's findings translates into a feedback sensitivity factor <m>\xi</m> of 0.03 KW-1m2> (assuming a climate sensitivity <m\Delta T_{2x}</m>} of 3<m>\circ</m>C. Note that this scaling convention (A51) ensures that climate sensitivities are comparable for the equilibrium warming that corresponds to twice preindustrial CO_2 concentration levels (see Table. 3 in http://www.atmos-chem-phys.net/11/1417/2011/acp-11-1417-2011.html).
Efficacies
Efficacy is defined as the ratio of global-mean temperature response for a particular radiative forcing divided by the global-mean temperature response for the same amount of global-mean radiative forcing induced by CO_2 (see Sect. 2.8.5 in Forster et al., 2005). In most cases, the efficacies are different for different forcing agents because of the geographical and vertical distributions of the forcing (Boer and Yu, 2003;Joshi et al., 2003;Hansen et al., 2005). The effective radiative forcing (<m>\Delta Q_e</m>) is the product of the standard climate forcing (<m>\Delta Q_a</m>), calculated after thermal adjustment of the stratosphere, and the efficacy (E<m>_a</m>). It is the effective forcings that are used in the energy balance equation (Eq.1), although both effective and standard forcings are carried through in the MAGICC code. Note that this parameterization yields slightly faster transient climate responses compared to an approach where different climate sensitivities are applied for each individual forcing agent (cf.Accounting for climate-state dependent feedbacks above).
In MAGICC, forcings for some components differ by hemisphere and over land and ocean. Just as for the global sensitivity, this, in combination with different land/ocean feedback factors, results in MAGICC6 exhibiting efficacies different from unity for non-CO_2 forcing agents. In other words, efficacies different from unity are in part a consequence of the geometric effect described above. MAGICC calculates these internal efficacies using reference year (default 2005) forcing patterns. After normalizing these forcing patterns to a global-mean of <m>\Delta Q_{2x}</m> (default 3.71 Wm-2), the internal efficacy can be determined as
<m>E_{\rm int} = \frac{\Delta T_{\rm eff2x}}{\Delta T_{2x}}\label{eq_efficacies_internal}</m>where <m>T_{\rm eff2x}</m> is the actual global-mean equilibrium temperature change resulting from a normalized forcing pattern and <m>\Delta T_{2x}</m> is the corresponding warming for 2x CO_2 forcing, i.e., the climate sensitivity. For most forcing agents, these internal efficacies are very close to one, except for forcings with a strong land/ocean forcing contrast, such as aerosol forcings. For example, for direct aerosol forcing in the HadCM3 emulation (calibration III - see Table B3 in http://www.atmos-chem-phys.net/11/1417/2011/acp-11-1417-2011.html) the efficacy is 1.14. By default, these internal efficacies are taken into account when applying prescribed efficacies, so that:
<m>\Delta Q_e = \frac{E_a}{E_{\rm int}}\Delta Q_a \label{eq_efficacies_acc_for_intefficacies}</m>The upwelling-diffusion equations
The transient temperature change evolution is largely influenced by the climate system's inertia, which in turn depends on the nature of the heat uptake by the climate system. The transient energy balance equations can be written as:
<m>f_{\rm NO}(\zeta_o \frac{d\Delta T_{\rm NO,1}}{dt}-\Delta Q_{\rm NO}+\lambda_o \alpha \Delta T_{\rm NO,1} + F_{N}) =k_{\rm LO}(\Delta T_{\rm NL} - \mu\alpha\Delta T_{\rm NO,1})+k_{NS}\alpha(\Delta T_{\rm SO,1} - \Delta T_{\rm NO,1})\label{eq_transient_linear_equations_NO}</m>
where the adjustment factor <m>\alpha</m> (default 1.2) determines - over ocean areas - the ratio of hemispheric changes in air (<m>\Delta T_{\rm xO}</m>) versus ocean mixed layer temperatures (<m>\Delta T_{\rm xO,1}</m>). Based on ECHAM1/LSG analysis (Raper and Cubasch, 1996), this sea-ice factor was first introduced by Raper et al. (2001) to account for the fact that the air temperature will exhibit additional warming, because the atmosphere feels warmer ocean surface temperatures where sea ice retreats. The bulk heat capacity of the mixed layer in each hemisphere x is <m>f_x\zeta_o=f_x\rho c h_m</m>, where <m>\rho</m> denotes the density of seawater (1.026<m>\times</m>106 g m-3), c is the specific heat capacity (0.9333 cal g-1<m>\circ</m>C-1= 4.1856<m>\times</m>0.9333 Joule g-1<m>\circ</m>C-1) and <m>h_m</m> is the mixed layer's thickness [m]. The bulk heat capacity of the land areas is <m>f_x\zeta_L</m>, here assumed to be zero. The net heat flux into the ocean below the mixed layer is denoted by <m>F_x</m>.
Equation (A55) can then be written as:
<m>\Delta T_{\rm NL} = \frac{f_{\rm NL}\Delta Q_{\rm NL}+k_{\rm LO}\mu\alpha\Delta T_{\rm NO,1}}{f_{\rm NL}\lambda_L + k_{\rm LO}}\label{eq_transient_separating_TNL}</m>Substituting <m>\Delta T_{\rm NL}</m> in Eq. (A55) yields:
<m>f_{\rm NO}(\zeta_o \frac{d\Delta T_{\rm NO,1}}{dt} - \Delta Q_{\rm NO} + \lambda_o \alpha\Delta T_{\rm NO,1} + F_N) = \frac{k_{\rm LO}}{\frac{k_{\rm LO}}{f_{\rm NL}}+\lambda_L}(\Delta Q_{\rm NL}-\lambda_L\mu\alpha \Delta T_{\rm NO,1})+ k_{\rm NS}\alpha(\Delta T_{\rm SO,1} - \Delta T_{\rm NO,1})\label{eq_transient_TNL_into_TNO}</m>Provided we know the heat flux <m>F_N</m> into the ocean below the mixed layer, we could now derive <m>d\Delta T_{\rm NO,1}/dt</m>. The net heat flux <m>F_N</m> at the bottom of the mixed layer is determined by vertical heat diffusivity (diffusion coefficient <m>K_z</m> [cm2s-1=3155.76-1m2yr-1]), and upwelling and downwelling (upwelling velocity w [m yr-1]), both acting on the perturbations <m>\Delta T</m> from the initial temperature profile <m>T^0_{\rm NO,z}</m>. If the upwelling rate <m>w</m> varies over time, the change in upwelling velocity <m>\Delta w^t{=}(w^t-w^0)</m> compared to its initial state <m>w^0</m> is assumed to act on the initial temperature profile, so that:
<m>F_N = \frac{K_z}{0.5h_d}\rho c (\Delta T_{\rm NO,1}-\Delta T_{\rm NO,2})- w \rho c (\Delta T_{\rm NO,2} - \beta \Delta T_{\rm NO,1})</m><m>- \Delta w \rho c (T^0_{\rm NO,2}- T^0_{\rm NO,sink})\label{eq_transient<m>eatflux_bottom_mixedlayer}</m>
where <m>T^0_{\rm NO,z}</m> is the initial temperature for water in layer z or in the downwelling pipe (z="sink").
Given that the top layer is assumed to be mixed, the gradient of the temperature perturbations is calculated by the difference of the perturbations divided by half the thickness <m>h_d</m> of the second layer (see Fig. A2). Substituting <m>F_N</m> in Eq.(A59 with Eq.(A60) and transforming the equation to discrete time steps, yields:
| <m>\frac{d\Delta T_{\rm NO,1}}{dt} \approx \frac{\Delta T_{\rm NO,1}^{t+1} - \Delta T_{\rm NO,1}^{t}}{\Delta t} =</m> | (A61)
|
| <m>\frac{1}{\zeta_o}\Delta Q_{\rm NO}^t </m> | <m>\textrm{:forcing} </m> |
| <m>- \frac{\lambda_o \alpha}{\zeta_o}\Delta T_{\rm NO,1}^{t+1} </m> | <m>\textrm{:feedback}</m> |
| <m>-\frac{K_z}{0.5h_d h_m}(\Delta T_{\rm NO,1}^{t+1}-\Delta T_{\rm NO,2}^{t+1}) </m> | <m>\textrm{:diffusion}</m> |
| <m>+ \frac{w^{t}}{h_m}(\Delta T^{t+1}_{\rm NO,2}-\beta \Delta T^{t+1}_{\rm NO,1}) </m> | <m>\textrm{:upwelling}</m> |
| <m>+ \frac{\Delta w^{t}}{h_m}(T^{0}_{\rm NO,2}-T^{0}_{\rm NO,sink}) </m> | <m>\textrm{:variable upwelling} </m> |
| <m>+ \frac{k_{\rm LO}(\Delta Q^{t}_{\rm NL}-\lambda_L \mu\alpha\Delta T^{t+1}_{\rm NO,1})}{\zeta_o f_{\rm NO}(\frac{k_{\rm LO}}{f_{\rm NL}}+\lambda_L)} </m> | <m>\textrm{:land forcing}</m> |
| <m>+ \frac{k_{\rm NS}\alpha}{\zeta_o f_{\rm NO}}(\Delta T_{\rm SO,1}^{t}-\Delta T_{\rm NO,1}^{t}) </m> | <m>\textrm{:inter-hemispheric ex.} </m> |
For the layers below the mixed layer (2<m>\leq</m>z<m>\leq</m>n-1), the temperature updating is governed by diffusion (first two terms in Eq.A62 and upwelling (last two terms), so that:
<m>\frac{\Delta T^{t+1}_{\rm NO,z}-\Delta T^{t}_{\rm NO,z}}{\Delta t}= \frac{K_z}{0.5(h_d+h_d')h_d}(\Delta T^{t+1}_{\rm NO,z-1}-\Delta T^{t+1}_{\rm NO,z})- \frac{K_z}{h_d^2}(\Delta T^{t+1}_{\rm NO,z}-\Delta T^{t+1}_{\rm NO,z+1})</m><m>+ \frac{w^{t}}{h_d}(\Delta T^{t+1}_{\rm NO,z+1}-\Delta T^{t+1}_{\rm NO,z})+ \frac{\Delta w^{t}}{h_d}(T^0_{\rm NO,z+1}-T^0_{\rm NO,z})\label{eq_transient_discrete_NO_submixed}</m>
where <m>h_d'</m> is zero for the layer below the mixed layer (z=2) and <m>h_d</m> otherwise, <m>\Delta w^t</m> is the change from the initial upwelling rate.
For the bottom layer (z=n), the downwelling term has to be taken into account, so that:
<m>\frac{\Delta T^{t+1}_{\rm NO,n}-\Delta T^{t}_{\rm NO,n}}{\Delta t}= \frac{K_z}{h_d^2}(\Delta T^{t+1}_{\rm NO,n-1}-\Delta T^{t+1}_{\rm NO,n})</m>
<m>+ \frac{w^{t}}{h_d}(\beta\Delta T^{t}_{\rm NO,1}-\Delta T^{t+1}_{\rm NO,n})+ \frac{\Delta w^{t}}{h_d}(T^0_{\rm NO,sink}-T^0_{\rm NO,n})\label{eq_transient_discrete_NO_bottom}</m>
Corresponding to the temperature calculations shown here for the Northern Hemisphere ocean (NO), the equivalent steps apply for the Southern Hemisphere ocean (SO). For simplicity, the equations described above are for the constant-depth area profile case, which MAGICC defaults to when the depth-dependency factor <m>\vartheta</m> is set to zero. The detailed code for the general case with <m>0{\leq}\vartheta{\leq}1</m> is given in the (Implementation of upwelling-diffusion-entrainment equations) section.
Calculating heat uptake
Heat uptake by the climate system can be calculated in different ways. One method is to use the global energy balance (Eq.1). Using the effective sensitivity as in (Eq.1) the heat uptake <m>F^t</m> is estimated as:
<m>{dH^t}{dt}=F^t = \Delta Q^t-(f_L \lambda_L \Delta T^t_{L} + f_O \lambda_O \Delta T^t_{O}) \label{eq<m>eatuptake_balance}</m>For verification purposes MAGICC6 calculates heat uptake in two ways, both directly (as above) and by integrating heat content changes in each layer in the ocean (yielding identical results), given the assumed zero heat capacity of the atmosphere and land areas:
<m>\Delta H^t = \sum^{n}_{i=1} \frac{1}{\rho c h_i}\frac{(f_{\rm NO}\Delta T^t_{\rm NO,i} + f_{\rm SO} \Delta T^t_{\rm SO,i})}{f_O}+\epsilon \label{eq<m>eatuptake_integrating}</m>where <m>h_i</m> is the thickness of the layer, i.e., <m>h_m</m> for the mixed layer and <m>h_d</m> for the others and <m>\epsilon</m> is a small term to account for the heat content of the polar sinking water.
Depth-dependent ocean with entrainment
Harvey and Schneider (1985b,a) introduced the upwelling-diffusion model with entrainment from the polar sinking water by varying the upwelling velocity w with depth. Building on the work by Raper et al. (2001), MAGICC6 also includes the option of a depth-dependent ocean area profile. If the depth-dependency parameter <m>\vartheta</m> is set to 1 (default), a standard depth-dependent ocean area profile is assumed as in HadCM2 and used in Raper et al. (2001)}. A constant upwelling velocity is assumed and mass conservation is maintained by "entrainment" from the downwelling pipe. With ocean area decreasing with depth and constant upwelling velocity, the upwelling mass flux would also have to decrease with depth. To offset this, the amount of entrainment into layer z is assumed to be proportional to the decrease in area from the top to the bottom of each layer (cf. Fig-A4). We differ from the model structures tested by Raper et al. (2001), by equating changes in the temperature of the entraining water to those in the downwelling pipe, namely a fraction <m>\beta</m> (default 0.2) of the mixed layer temperature <m>\Delta T_{x,1}^{t-1}</m> of the previous timestep in Hemisphere x. For a detailed description of the code, see the following Sect. Implementation of upwelling-diffusion-entrainment equations. Simple upwelling-diffusion models can overestimate the ocean heat uptake for higher warming scenarios when applying parameter values calibrated to match heat uptake for lower warming scenarios (see e.g. Fig. 17b in Harvey et al., 1997). To address this, MAGICC6 includes a warming-dependent vertical diffusivity gradient. The physical reasoning is that a strengthened thermal stratification and, hence, reduced vertical mixing leads to decreased heat uptake for higher warming. Thus, the effective vertical diffusivity at <m>K_{z,i}</m> between ocean layer i and i+1 is given by:
<m>K_{z,i} = {\rm max}\,(K_{z,{\rm min}}(1 - d_i)\frac{dK_{\rm z}}{dT}(\Delta T_{H,1}^{t-1}-\Delta T_{H,n}^{t-1})+K_z) \label{eq_verticalDiffusivity<m>eatdependent}</m>where <m>K_{z,{\rm min}}</m> is the minimum vertical diffusivity (default 0.1 cm2 s-1); <m>d_i</m> is the relative depth of the layer boundary with zero at the bottom of the mixed layer and one for the top of the bottom layer; <m>\frac{dK_{\rm z}}{dT}</m> is a newly introduced ocean stratification coefficient specifying how the vertical diffusivity <m>K_{\rm z}</m> between the mixed layer 1 and layer 2 changes with a change in the temperature difference between the top/mixed and bottom ocean layer of the respective hemisphere at the previous timestep t-1 <m>(\Delta T_{H,1}^{t-1}{-}\Delta T_{H,n}^{t-1})</m>.