Difference between revisions of "The Carbon Cycle"
(Created page with "*model description ** carbon cycle ** non-CO2 concentrations **[[Radiative Forcing | radiative forcing r...") |
(No difference)
|
Revision as of 13:15, 17 June 2013
Contents
The carbon cycle
Changes in atmospheric CO2 concentration, C, are determined by CO2 emissions from fossil and industrial sources (<m>E_{\rm foss}</m>), other directly human-induced CO2 emissions from or removals to the terrestrial biosphere (<m>E_{\rm lu}</m>), the contribution from oxidized methane of fossil fuel origin (<m>E_{\rm fCH_4},</m>), the flux due to ocean carbon uptake (<m>F_{\rm ocn}</m>) and the net carbon uptake or release by the terrestrial biosphere (<m>F_{\rm terr}</m>) due to CO2 fertilization and climate feedbacks. As in the C4MIP generation of carbon cycle models, no nitrogen or sulphur deposition effects on biospheric carbon uptake are included here Thornton et al., 2006. Hence, the budget Eq.A1 for a change in atmospheric CO2 concentrations is:
<m>\Delta C/\Delta t= E_{\rm foss} + E_{\rm lu} + E_{\rm fCH_4}- F_{\rm ocn} - F_{\rm terr}</m>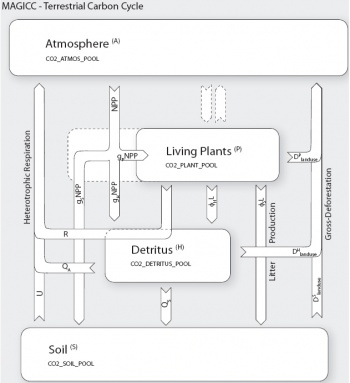
Terrestrial carbon cycle
The terrestrial carbon cycle follows that in Wigley, 1993, in turn is based on Harvey, 1989. It is modeled with three boxes, one living plant box <m>P</m> (see Fig.Terrestrial Carbon Cycle) and two dead biomass boxes, of which one is for detritus <m>H</m> and one for
organic matter in soils <m>S</m>. The plant box comprises woody material, leaves/needles, grass, and roots, but does not include the rapid turnover part of living biomass, which can be assumed to have a zero lifetime on the timescales of interest here (dashed extension of plant box <m>P</m> in Fig.Fig-A2. Thus, a fraction of gross primary product (GPP) cycles through the plant box directly back to the atmosphere due to autotrophic respiration and can be ignored (dashed arrows). Only the remaining part of GPP, namely the net primary production (NPP) is simulated. The NPP flux is channeled through the ``rapid turnover´´ part of the plant box and partitioned into carbon fluxes to the remainder plant box (default <m>g_P</m>=35%), detritus (<m>g_H</m>=60%) and soil box
(<m>g_S</m>=1-<m>g_P</m>-<m>g_H</m>=5%).
The plant box has two decay terms, litter production <m>L</m> and a part of gross deforestation <m>D_{\rm gross}^P</m>. Litter production is partitioned to both the detritus (<m>\phi_H</m>=98%) and soil box (<m>\phi_S</m>=1-<m>\phi_H</m>=2%). Thus, the mass balance for the plant box is:
<m>\Delta P/\Delta t = g_P{\rm NPP} - R - L - D_{\rm gross}^P \label{eq_massbalance_P}</m>The detritus box has sources from litter production (<m>\phi_HL</m>) and sinks to the atmosphere due to land use (<m>D_{\rm lu}^H</m>), non-land use related oxidation (<m>Q_A</m>), and a sink to the soil box (<m>Q_S</m>). The mass balance for the detritus box is thus
<m> \Delta H/\Delta t = g_H{\rm NPP} + \phi_H L - Q_A - Q_S - D_{\rm lu}^H \label{eq_massbalance_H}</m>The soil box has sources from litter production (<m>\phi_S</m>L), the detritus box (<m>Q_S</m>) and fluxes to the atmosphere due to land use (<m>D_{\rm gross}^S</m>), and non-land use related oxidation (<m>U</m>). The mass balance for the soil box is thus
<m> \Delta S/\Delta t = g_S{\rm NPP} +\phi_S L + Q_S - U - D_{\rm lu}^S \label{eq_massbalance_S}</m>The decay rates (<m>L</m>, <m>Q</m> and <m>U</m>) of each pool are assumed to be proportional to pool's box masses <m>P</m>, <m>H</m> and <m>S</m>, respectively. The turnover times <m>\tau_P</m>, <m>\tau_H</m> and <m>\tau_S</m> are determined by the initial steady-state conditions for box sizes and fluxes.
<m>L_0 = P_0/\tau^P_0</m>
Constant relaxation times <m>\tau</m> ensure that the box masses will relax back to their initial sizes if perturbed by a one-off land use change-related carbon release or uptake -- assuming no changes in fertilization and temperature feedback terms. This relaxation acts as an effective regrowth term so that deforestation <m>\Sigma D_{\rm gross}{=}D_{\rm gross}^P + D_{\rm gross}^H + D_{\rm gross}^S</m> represents the gross land use emissions, related to net land use emissions <m>E_{\rm lu}</m> by regrowth <m>\Sigma G</m>=<m>G^P</m> + <m>G^H</m> + <m>G^S</m>
<m>\Sigma D_{\rm gross} - \Sigma {\rm G} = E_{\rm lu}</m>
Gross land-use related emissions might be smaller (compared to a case where relaxation times are assumed constant) as some human land use activities, e.g.\ deforestation, can lead to persistent changes of the ecosystems over the time scales of interest, thereby preventing full regrowth to the initial state <m>P_0</m>, <m>H_0</m> or <m>S_0</m>. A factor <m>\psi</m> is used to denote the fraction of gross deforestation that does not regrow (0<m>{\leq}{\psi}{\leq}</m>1). Thus, the relaxation times <m>\tau</m> are made time-dependent according to the following equation:
<m>\tau^P(t) = \left(P_0 - \psi\int_0^t d_PE_{\rm lu}(t')dt'\right)/L_0</m>
Formulation for CO2 fertilization
CO2 fertilization indicates the enhancement in net primary production (NPP) due to elevated atmospheric CO2 concentration. As described in Wigley, 2000, there are two common forms used in simple models to simulate the CO2 fertilization effect: (a) the logarithmic form (fertilization parameter <m>\beta_m</m>=1) and (b) the rectangular hyperbolic or sigmoidal growth function (<m>\beta_m</m>=2) (see e.g. Gates, 1985. The rectangular hyperbolic formulation provides more realistic results for both low and high concentrations so that NPP does not rise without limit as CO2 concentrations increase. Previous MAGICC versions include both formulations, but used the second as default. The code now allows use of a linear combination of both formulations (1<m>{\leq}{\beta_m}{\leq}</m>2).
The classic logarithmic fertilization formulation calculates the enhancement of NPP as being proportional to the logarithm of the change in CO2 concentrations C above the preindustrial level <m>C_0</m>:
<m>\beta_{\rm log}=1 + \beta_s \,{\rm ln}\,({\rm C/C}_0) \label{eq_CO2fertilization_logarithm}</m>The rectangular hyperbolic parameterization for fertilization is given by
<m>N=\frac{{C-C}_b}{1+b({C-C}_b)}</m>
- <m>=\frac{{N_0}(1+b(C_0-C_b))({C}-{C_b})}{(C_0-C_b)(1+b({C-C}_b))}\label{eq_CO2fertilization_sigmoidal growth}</m>(A16)
where <m>N_0</m> is the net primary production and <m>C_0</m> the CO2 concentrations at pre-industrial conditions, <m>C_b</m> the concentration value at which NPP is zero (default setting: <m>C_b</m>=31 ppm, see Gifford, 1993.
For better comparability with models using the logarithmic formulation, following Wigley, 2000, the CO2 fertilization factor <m>\beta_s</m> expresses the NPP enhancement due to a CO2 increase from 340 ppm to 680 ppm, valid under both formulations. Thus, MAGICC first determines the NPP ratio <m>r</m> for a given <m>\beta_s</m> fertilization factor according to:
<m>r=\frac{{N}(680)}{{N}(340)}=\frac{{N}_0(1+\beta_s \,{\rm ln}\,(680/Template:C_0))}{{N}_0(1+\beta_s \,{\rm ln}\, (340/{C}_0))}\label{eq_CO2fertilization_340to640}</m>Following from here, <m>b</m> in Eq. A16 is determined by
<m>b=\frac{(680-{C}_b)-r(340-{C}_b)}{(r-1)(680-{C}_b)(340-{C}_b)}\label{eq_CO2fertilization_determining b}</m>which can in turn be used in Eq. A16 to calculate the effective CO2 fertilization factor <m>\beta _{\rm sig}</m> at time <m>t</m> as
<m>\beta _{\rm sig}(t)=\frac{1/({C}_0 - {C}_b) + b}{1/({C}(t)- {C}_b) + b} \label{eq_CO2fertilization_factor_michaelismenton}</m>MAGICC6 allows for an increased flexibility, as any linear combination between the two fertilization parameterizations can be chosen (1<m>{\leq}{\beta_m}{\leq}</m>2), so that the effective fertilization factor <m>\beta _{\rm eff}</m> is given by:
<m>\beta _{\rm eff}(t)=(2-\beta_m)\beta_{\rm log}+(\beta_m-1)\beta_{\rm sig}\label{eq_CO2fertilization_factor_effective}</m>The CO2 fertilization effect affects NPP so that <m>\beta_{\rm eff}</m> = NPP - NPP0. MAGICC's terrestrial carbon cycle furthermore applies the fertilization factor to one of the heterotrophic respiration fluxes <m>R</m> that cycles through the detritus box, which makes up 18.5 % of the total heterotrophic respiration (<m>\sum {\rm R} {=} R+U_a+Q</m>) at the initial steady-state.
Temperature effect on respiration and decomposition
Global-mean temperature increase is taken as a proxy for climate-related impacts on the carbon cycle fluxes induced by regional temperature, cloudiness or precipitation regime changes. Those impacts are commonly referred to as ``climate feedbacks on the carbon cycle´´, or simply, ``carbon cycle feedbacks´´. Here, the terrestrial carbon fluxes NPP, and the heterotrophic respiration/decomposition fluxes <m>R</m>, <m>Q</m> and <m>U</m> are scaled assuming an exponential relationship,
<m>F_{i}(t)= F_{i}'(t)\cdot {\rm exp}(\sigma_{i}\Delta T(t))\label{eq_CO2feedback_GPP}</m>where <m>\Delta T(t)</m> is the temperature above a reference year level, e.g. for 1990 or 1900, and <m>F_i'</m> (<m>F_i</m>) stands for the (feedback-adjusted) fluxes NPP, <m>R</m>, <m>Q</m> and <m>U</m>. The parameters <m>\sigma_i</m> (K<m>^{-1}</m>) are their respective sensitivities to temperature changes. In order to model the actual change in <m>Q</m> and <m>U</m>, the relaxation times <m>\tau</m> for the detritus and soil pool are adjusted, respectively. Land use CO2 emissions in many emissions scenarios (e.g SRES, Nakicenovic and Swart, 2000) reflect the net directly human-induced emissions. At each time-step, the gross land use emissions are subtracted from the plant, detritus and soil carbon pools. The difference between net and gross land use emissions is the CO2 uptake due to regrowth. Thus, a separation between directly human-induced (deforestation-related) emissions and indirectly human-induced effects (regrowth) on the carbon cycle is required. As both regrowth and the temperature sensitivity are modeled by adjusting the turnover times, a no-feedback case is computed separately, retrieving the regrowth, then calculating the feedback-case including the formerly calculated regrowth.
Ocean carbon cycle
For modeling the perturbation of ocean surface dissolved inorganic carbon, an efficient impulse response substitute for the 3D-GFDL model Sarmiento et al. (1992) is incorporated into MAGICC. The applied analytical representation of the pulse response function is provided in Appendix A.2.2 of Joos et al. (1996).
The sea-to-air flux <m>F_{\rm ocn}</m> is determined by the partial pressure differential for CO2 between the atmosphere C and surface layer of the ocean <m>\rho</m>CO2
<m>{\rm F}_{\rm ocn} = k (C-\rho {\rm CO}_2) \label{eq_fluxocean}</m>where <m>k</m> is the global average gas exchange coefficient (Joos et al., 2001). This exchange coefficient is here calibrated to the individual C<m>^4</m>MIP carbon cycle models (default value (7.66 yr-1). The perturbation in dissolved inorganic carbon in the surface ocean <m>\Delta\Sigma {\rm CO_2}(t)</m> at any point t in time is obtained from the convolution integral of the mixed layer impulse response function <m>r_s</m> and the net air-to-sea flux <m>F_{\rm ocn}</m>:
<m>\label{eq_hilda_pertdissolvedinorgCO2}\Delta\Sigma {\rm CO_2}(t) &=& \frac{c}{hA}\{\int_{t_0}^{t} {F}_{\rm ocn}(t') r_s(t-t')dt')\}</m>The impulse response function <m>r_s</m> is given for the time immediately after the impulse injection (<1 yr) by (see Appendix A.2.4 of Joos et al., 1996):
<m>r_s(t)&=& 1.0 - 2.2617t + 14.002t^2-48.770t^3+82.986t^4-67.527t^5+21.037t^6 \label{eq_hilda_impulseresponse_below2years}</m>and for t<m>{\geq}</m>1 year is given by:
<m>r_s(t)= \sum_{i=1}^6 \gamma_i e^{-\tau_i t}\label{eq_oceancc_after_initialphase}</m>with the partitioning <m>\gamma</m> and relaxation <m>\tau</m> coefficients:
<m>\gamma=\left[\begin{array}{l}0.01481\\0.70367\\0.24966\\0.066485\\0.038344\\0.019439\end{array}\right]\tau=\left[\begin{array}{l}0\\1/0.70177\\1/2.3488\\1/15.281\\1/65.359\\1/347.55\end{array}\right] \label{eq_hilda_impulseresponse_after2years_coefficients}</m>The relationship between the perturbation to dissolved inorganic carbon <m>\Delta\Sigma</m>CO<m>_2(t)</m> and ocean surface partial pressures <m>\Delta\rho</m>CO2(<m>T_0</m>) (expressed in ppm or <m>\mu</m>atm) at the preindustrial temperature level <m>T_0</m> is given by Eq.(A23) in Joos et al. (1996). Furthermore, the temperature sensitivity effect on CO2 solubility and hence oceanic carbon uptake is parameterized with a simple exponential expression. The modeled partial pressure <m>\rho</m>CO<m>_2(t)</m> increases with sea surface temperatures according to:
<m>\rho {\rm CO}_2(t) = [\rho {\rm CO}_2(t_0) + \Delta\rho {\rm CO}_2(T_0)]\, {\rm exp}(\alpha_T \Delta T)\label{eq_partialpressure_ocn}</m>where <m>\alpha_T</m> (default <m>\alpha_T</m>=0.0423 K-1) is the sensitivity of the sea surface partial pressure to changes in temperature (<m>\Delta T</m>) away from the preindustrial level (see Eq.(A24) in Joos et al. (1996), based on Takahashi et al. (1993)).