Difference between revisions of "Model Description"
(Created page with "*model description ** carbon cycle ** non-CO2 concentrations **[[Radiative Forcing | radiative forcing r...") |
(No difference)
|
Revision as of 12:20, 17 June 2013
- model description
Contents
Model description
Overview
The 'Model for the Assessment of Greenhouse Gas Induced Climate Change' (MAGICC) is a simple/reduced complexity climate model. MAGICC was originally developed by Tom Wigley (National Centre for Atmospheric Research, Boulder, US, and University of Adelaide, Australia) and Sarah Raper (Manchester Metropolitan University, UK) in the late 1980s and continuously developed since then. It has been one of the widely used climate models in various IPCC Assessment Reports. The latest version, MAGICC6, is co-developed by Malte Meinshausen (Potsdam Institute for Climate Impact Research, Germany, and the University of Melbourne, Australia). These pages provide an extensive model description, sourced from a 2011 publication in Atmospheric Chemistry & Physics (M. Meinshausen, S. Raper and T. Wigley, 2011).
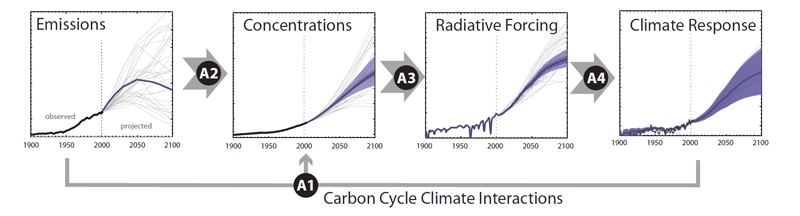
This Page provides a detailed description of MAGICC6 and its different modules (see Fig-A1 below). A basic model description is given, while subsections describe MAGICC's carbon cycle, the atmospheric-chemistry parameterizations and derivation of non-CO2 concentrations, radiative forcing routines, and the climate module to get from radiative forcing to hemispheric (land and ocean, separately) to global-mean temperatures (climate model), as well as oceanic heat uptake. Finally, details are provided on the implementation scheme for the upwelling-diffusion-entrainment ocean climate module. A technical upgrade is that MAGICC6 has been re-coded in Fortran95, updated from previous Fortran77 versions. Nearly all of the MAGICC6 code is directly based on the earlier MAGICC versions programmed by Wigley and Raper ( 1987, 1992, 2001).
Basic model description
MAGICC has a hemispherically averaged upwelling-diffusion ocean coupled to an atmosphere layer and a globally averaged carbon cycle model. As with most other simple models, MAGICC evolved from a simple global average energy-balance equation. The energy balance equation for the perturbed climate system can be written as:
<m>\Delta Q_G = \lambda_G \Delta T_G + \frac{d H}{d t}\label{eq_globalenergybalance}</m>where <m>\Delta Q_G</m> is the global-mean radiative forcing at the top of the troposphere. This extra energy influx is partitioned into increased outgoing energy flux and heat content changes in the ocean <m>\frac{d H}{d t}</m>. The outgoing energy flux is dependent on the global-mean feedback factor, <m>\lambda_G</m>, and the surface temperature perturbation <m>\Delta T_G</m>.
While MAGICC is designed to provide maximum flexibility in order to match different types of responses seen in more sophisticated models, the approach in MAGICC's model development has always been to derive the simple equations as much as possible from key physical and biological processes. In other words, MAGICC is as simple as possible, but as mechanistic as necessary. This process-based approach has a strong conceptual advantage in comparison to simple statistical fits that are more likely to quickly degrade in their skill when emulating scenarios outside the original calibration space of sophisticated models.
The main improvements in MAGICC6 compared to the version used in the IPCC AR4 are briefly highlighted in this section (Note that there is an intermediate version, MAGICC 5.3, described in Wigley et al., 2009). The options introduced to account for variable climate sensitivities are described in Sect. introduction of variable climate sensitivities. With the exception of the updated carbon cycle routines updated carbon cycle, the MAGICC 4.2 and 5.3 parameterizations are covered as special cases of the 6.0 version, i.e., the IPCC AR4 version, for example, can be recovered by appropriate parameter settings.
Introduction of variable climate sensitivities
Climate sensitivity (<m>\Delta T_{2x}</m>) is a useful metric to compare models and is usually defined as the equilibrium global-mean warming after a doubling of CO<m>_2</m> concentrations. In the case of MAGICC, the equilibrium climate sensitivity is a primary model parameter that may be identified with the eventual global-mean warming that would occur if the CO<m>_2</m> concentrations were doubled from pre-industrial levels. Climate sensitivity is inversely related to the feedback factor <m>\lambda</m>:
<m>\label{eq_climatesensitivity}\Delta T_{2x} = \frac{\Delta Q_{2x}}{\lambda}</m>where <m>\Delta T_{2x}</m> is the climate sensitivity, and <m>\Delta Q_{2x}</m> the radiative forcing after a doubling of CO<m>_2</m> concentrations (see energy balance Eq. A45).
The (time- or state-dependent) effective climate sensitivity (<m>S^t</m>)(Murphy and Mitchell, 1995) is defined using the transient energy balance Eq. (1) and can be diagnosed from model output for any part of a model run where radiative forcing and ocean heat uptake are both known and their sum is different from zero, so that:
<m>\label{eq_effective_climatesensitivity} S^t = \frac{\Delta Q_{2x}}{\lambda^t} = \Delta Q_{2x} \frac{\Delta T_{G}^t}{\Delta Q^t - \frac{d H}{dt}|^t}</m>where <m>\Delta Q_{2x}</m> is the model-specific forcing for doubled CO<m>_2</m> concentration, <m>\lambda_t</m> is the time-variable feedback factor, <m>\Delta Q^t</m> the radiative forcing, <m>\Delta T_{GL}^t</m> the global-mean temperature perturbation and <m>\frac{dH}{dt}|^t</m> the climate system's heat uptake at time <m>t</m>. By definition, the traditional (equilibrium) climate sensitivity (<m>\Delta T_{2x}</m>) is equal to the effective climate sensitivity <m>S^t</m> at equilibrium (<m>\frac{dH}{dt}|^t</m>=0) after doubled (pre-industrial) CO<m>_2</m> concentration.
If there were only one globally homogenous, fast and constant feedback process, the diagnosed effective climate sensitivity would always equal the equilibrium climate sensitivity <m>\Delta T_{2x}</m>. However, many CMIP3 AOGCMs exhibit variable effective climate sensitivities, often increasing over time (e.g. models CCSM3, CNRM-CM3, GFDL-CM2.0, GFDL-CM2.1, GISS-EH - see Figs. (B1, B2, B3 in http://www.atmos-chem-phys.net/11/1417/2011/acp-11-1417-2011.html). This is consistent with earlier results of increasing effective sensitivities found by (Senior and Mitchell (2000);Raper et al. (2000)) for the HadCM2 model. In addition, some models present significantly higher sensitivities for higher forcing scenarios (1pctto4x) than for lower forcing scenarios (1pctto2x) (e.g. ECHAM5/MPI-OM and GISS-ER, see Fig.1
In order to better emulate these time-variable effective climate sensitivities, this version of MAGICC incorporates two modifications: Firstly, an amended land-ocean heat exchange formulation allows effective climate sensitivities to increase on the path to equilibrium warming. In this formulation, changes in effective climate sensitivity arise from a geometrical effect: spatially non-homogenous feedbacks can lead to a time-variable effective global-mean climate sensitivity, if the spatial warming distributions change over time. Hence, by modifying land-ocean heat exchange in MAGICC, the spatial evolution of warming is altered, leading to changes in effective climate sensitivities (Raper, 2004) given that MAGICC has different equilibrium sensitivities over land and ocean. Secondly, the climate sensitivities, and hence the feedback parameters, can be made explicitly dependent on the current forcing at time <m>t</m>. Both amendments are detailed in the Revised land-ocean heat formulation, and Accounting for climate-state dependent feedbacks sections. Although these two amendments both modify the same diagnostic, i.e., the time-variable effective sensitivities in MAGICC, they are distinct: the land-ocean heat exchange modification changes the shape of the effective climate sensitivity's time evolution to equilibrium, but keeps the equilibrium sensitivity unaffected. In contrast, making the sensitivity explicitly dependent on the forcing primarily affects the equilibrium sensitivity value.
Note that time-varying effective sensitivities are not only empirically observed in AOGCMs, but they are necessary here in order for MAGICC to accurately emulate AOGCM results. Alternative parameterizations to emulate time-variable climate sensitivities are possible, e.g.~assuming a dependence on temperatures instead of forcing, or by implementing indirect radiative forcing effects that are most often regarded as feedbacks see Section 6.2 in http://www.atmos-chem-phys.net/11/1417/2011/acp-11-1417-2011.html. However, this study chose to limit the degrees of freedom with respect to time-variable climate sensitivities given that a clear separation into three (or more) different parameterizations seemed unjustified based on the AOGCM data analyzed here.
Updated carbon cycle
MAGICC's terrestrial carbon cycle model is a globally integrated box model, similar to that in Harvey (1989) and Wigley (1993). The MAGICC6 carbon cycle can emulate temperature-feedback effects on the heterotrophic respiration carbon fluxes. One improvement in MAGICC6 allows increased flexibility when accounting for CO2 fertilization. This increase in flexibility allows a better fit to some of the more complex carbon cycle models reviewed in C<m>^4</m>MIP(Friedlingstein, 2006)(see terrestrial carbon cycle).
Another update in MAGICC6 relates to the relaxation in carbon pools after a deforestation event. The gross CO2 emissions related to deforestation and other land use activities are subtracted from the plant, detritus and soil carbon pools (see Fig. terrestrial carbon cycle]. While in previous versions only the regrowth in the plant carbon pool was taken into account to calculate the net deforestation, MAGICC6 now includes an effective relaxation/regrowth term for all three terrestrial carbon pools (see terrestrial carbon cycle).
The original ocean carbon cycle model used a convolution representation (Wigley, 1991) to quantify the ocean-atmosphere CO<m>_2</m> flux. A similar representation is used here, but modified to account for nonlinearities. Specifically, the impulse response representation of the Princeton 3D GFDL model (Sarmiento, 1992) is used to approximate the inorganic carbon perturbation in the mixed layer (for the impulse response representation see, Joos, 1991). The temperature sensitivity of the sea surface partial pressure is implemented based on Takahashi et al. (1993) as given in Joos et al. (2001). For details on the updated carbon cycle routines, see the The carbon cycle.
Other additional capabilities compared to MAGICC4.2
Five additional amendments to the climate model have been implemented in MAGICC6 compared to the MAGICC4.2 version that has been used in IPCC AR4.
Aerosol indirect effects
It is now possible to account directly for contributions from black carbon, organic carbon and nitrate aerosols to indirect (i.e., cloud albedo) effects (Twomey, 1977). The first indirect effect, affecting cloud droplet size and the second indirect effect, affecting cloud cover and lifetime, can also be modeled separately. Following the convention in IPCC AR4 (Forster et al., 2007), the second indirect effect is modeled as a prescribed change in efficacy of the first indirect effect. See Tropospheric aerosols for details.
Depth-variable ocean with entrainment
Building on the work by Raper et al. (2007), MAGICC6 includes the option of a depth-dependent ocean area profile with entrainment at each of the ocean levels (default, 50 levels) from the polar sinking water column. The default ocean area profile decreases from unity at the surface to, for example, 30<m>%</m>, 13<m>%</m> and 0<m>%</m> at depths of 4000, 4500 and 5000 m. Although comprehensive data on depth-dependent heat uptake profiles of the CMIP3 AOGCMs were not available for this study, this entrainment update provides more flexibility and allows for a better simulation of the characteristic depth-dependent heat uptake as observed in one analyzed AOGCM, namely HadCM2 (Raper et al., 2000).
Vertical mixing depending on warming gradient
Simple models, including earlier versions of MAGICC, sometimes overestimated the ocean heat uptake for higher warming scenarios when applying parameter sets chosen to match heat uptake for lower warming scenarios, see e.g. Fig. 17b in Harvey et al. (1997). A strengthened thermal stratification and hence reduced vertical mixing might contribute to the lower heat uptake for higher warming cases. To model this effect, a warming-dependent vertical gradient of the thermal diffusivity is implemented here(seeDepth-dependent ocean with entrainment).
Forcing efficacies
Since the IPCC TAR, a number of studies have focussed on forcing efficacies, i.e., on the differences in surface temperature response due to a unit forcing by different radiative forcing agents with different geographical and vertical distributions (Joshi et al., 1997). This version of MAGICC includes the option to apply different efficacy terms for the different forcings agents (see the efficacies section for details and supplement pdf in http://www.atmos-chem-phys.net/11/1417/2011/acp-11-1417-2011.html for default values).
Radiative forcing patterns
Earlier versions of MAGICC used time-independent (but user-specifiable) ratios to distribute the global-mean forcing of tropospheric ozone and aerosols to the four atmospheric boxes, i.e., land and ocean in both hemispheres. This model structure and the simple 4-box forcing patterns are retained as it is able to capture a large fraction of the forcing agent characteristics of interest here. However, we now use patterns for each forcing individually, and allow for these patterns to vary over time. For example, the historical forcing pattern evolutions for tropospheric aerosols are based on results from Hansen et al. (2005), which are interpolated to annual values and extrapolated into the future using hemispheric emissions. Additionally, MAGICC6 now incorporates forcing patterns for the long-lived greenhouse gases as well, although these patterns are assumed to be constant in time and scaled with global-mean radiative forcing (supplement pdf in http://www.atmos-chem-phys.net/11/1417/2011/acp-11-1417-2011.html for details on the default forcing patterns and time series).